Squares and trees
Propositions1
A proposition consists of a subject and a predicate linked with a verb (cupola). For example, the sentence “all horses are animals” can be broken down into the following components: “All horses (subject) are (cupola) animals (predicate)” This is an affirmative proposition. A negative proposition includes a form of negation, such as the word “no”. For example: “No horses are animals”. Propositions also vary in quantity. They can be universal, particular, indefinite or singular. “All horses are animals” is a universal affirmative proposition. “Some horses are not animals”, is a particular, negative proposition (and false!).
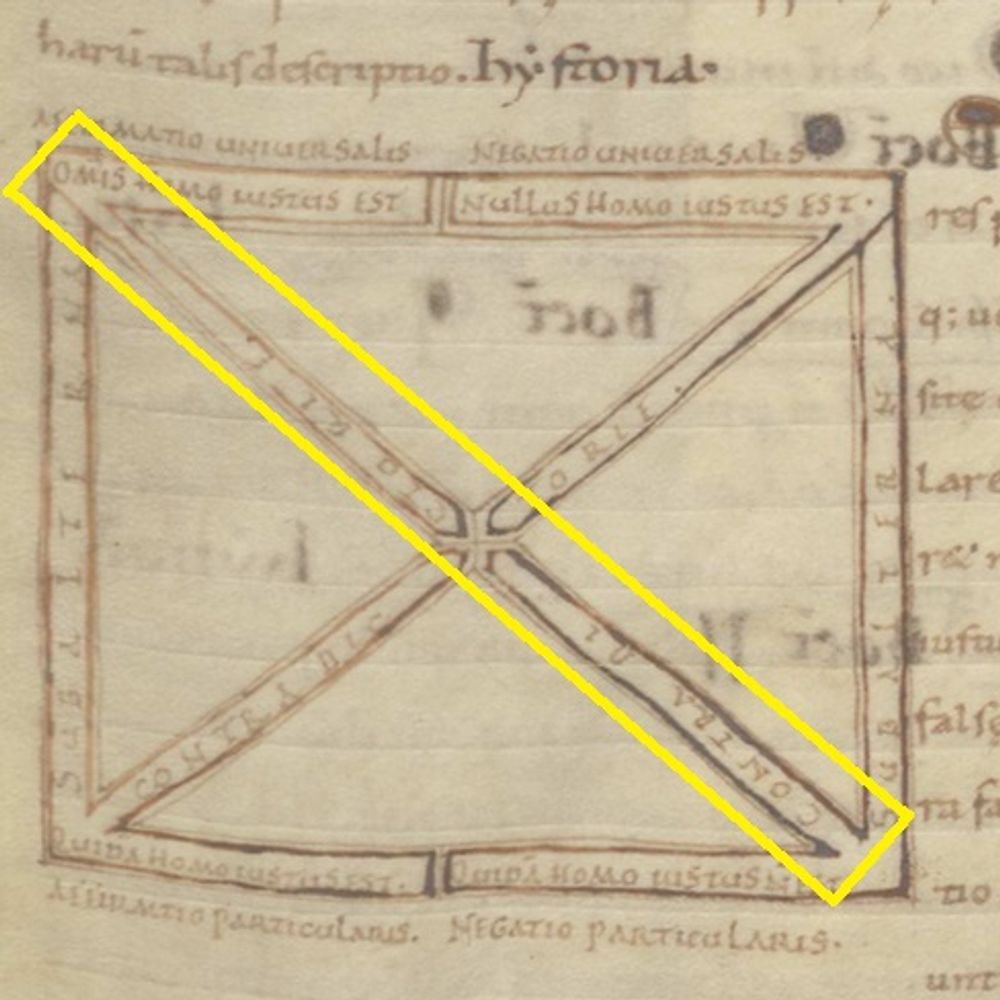
The Square of Opposition
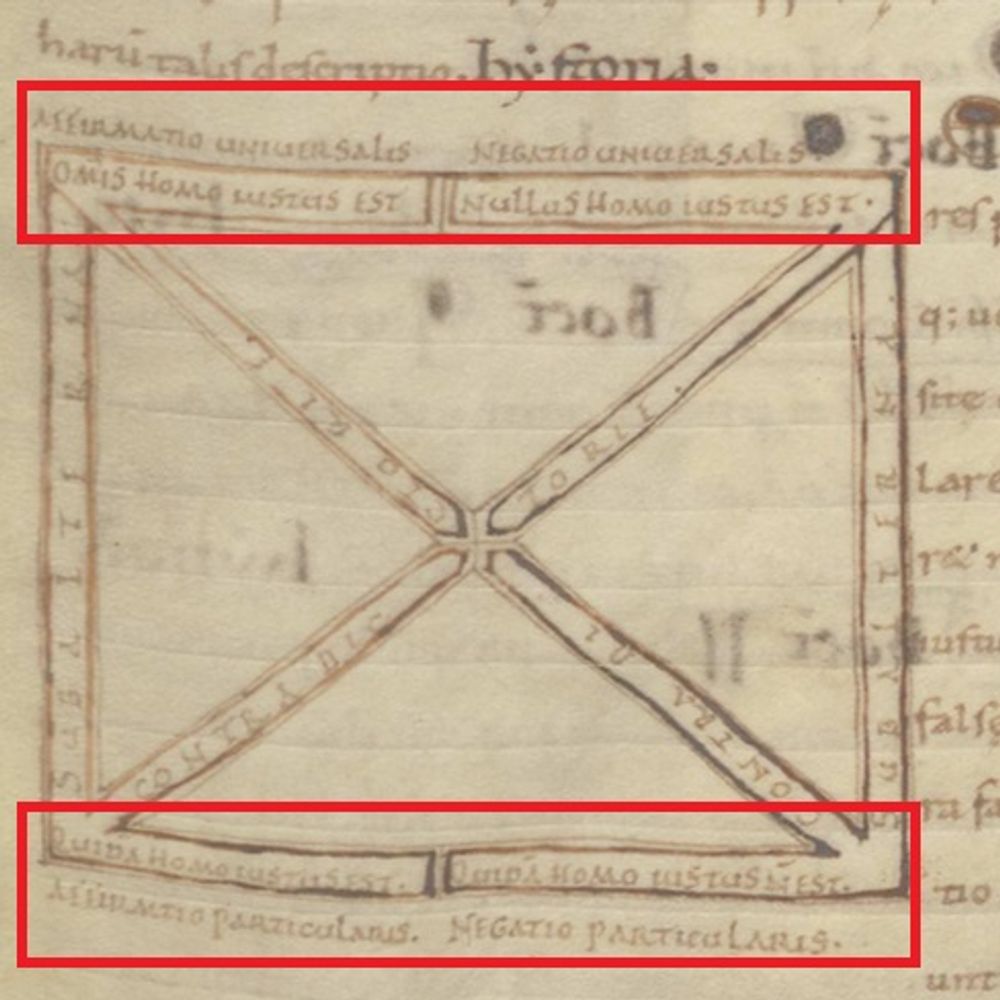
The square of opposition is a common diagram found in medieval dialectical manuscripts and is used to relate propositions to each other. It’s a sort of argument-tester which allows one to identify logical fallacies. We don’t know precisely who the first person to relate propositions in the form of a ‘square of opposition’ was, but the earliest examples are found in copies of the Peri hermeneias, a second-century text by the logician Apuleius. In this square of opposition found in Leiden, UB, BPL 25 (f. 12r), a copy of the Peri hermeneias, the proposition under examination is “All men are just”, “Omnis homo iustus est”. Click through the captions to the image to examine the different propositional relationships expressed in the square.
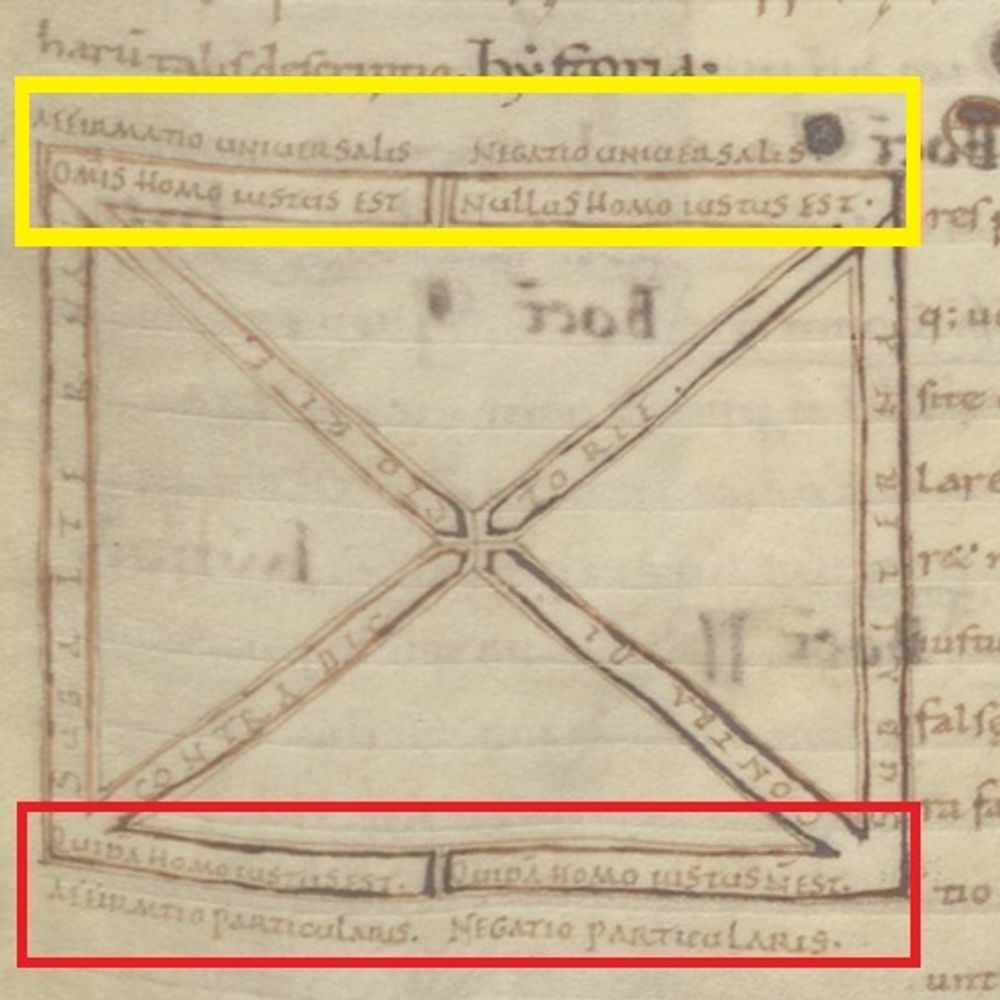

http://hdl.handle.net/1887.1/item:1617684
Buridan’s Octagon of Opposition
A particularly elaborated version of the square of opposition is found in Jean Buridan’s (c. 1301-60) Summulae de dialectica. Known as an ‘octagon of opposition’, Buridan – teacher at the Faculty of Arts at the University of Paris – here amends the traditional square to also incorporate modal syllogisms. A modal syllogism is one that uses the words ‘necessarily’, ‘possibly’, or ‘contingently’. For example, ‘just possibly applies to some men’, ‘just necessarily applies to no men’. By incorporating these extra sets of syllogisms, Buridan extended the number of relations which were possible in the traditional square. The octagon is only present in some of the manuscripts of the Summulae, so it may not have been an authorial addition, but it clearly was a useful addition for students grappling with more complex logical propositions.

https://gallica.bnf.fr/ark:/12148/btv1b90767401
Categories
In the Categories, Aristotle identifies ten categories (in Latin ‘praedicamenta’) which can be used to describe everything in the world:
Substance (e.g. a man, the species man, the genus animal)
Quantity (e.g. line, number)
Relation (e.g. larger)
Quality (e.g. sweetness)
Doing (e.g. cooling)
Undergoing (e.g. being cooled)
Place (e.g. in the market square)
Time (e.g. yesterday)
Position (e.g. sitting)
Having (e.g having shoes on)
The first category, substance, describes what something is, what is its being (e.g. ‘Socrates is a man’; being a man is fundamental to the essence of what it is to be Socrates). The remaining categories are ‘accidents’, these are the properties of the substance, they describe how something is, properties which are not necessarily essential to what it is (e.g. ‘Socrates is sitting’; Socrates could equally be standing, but he would still be Socrates).
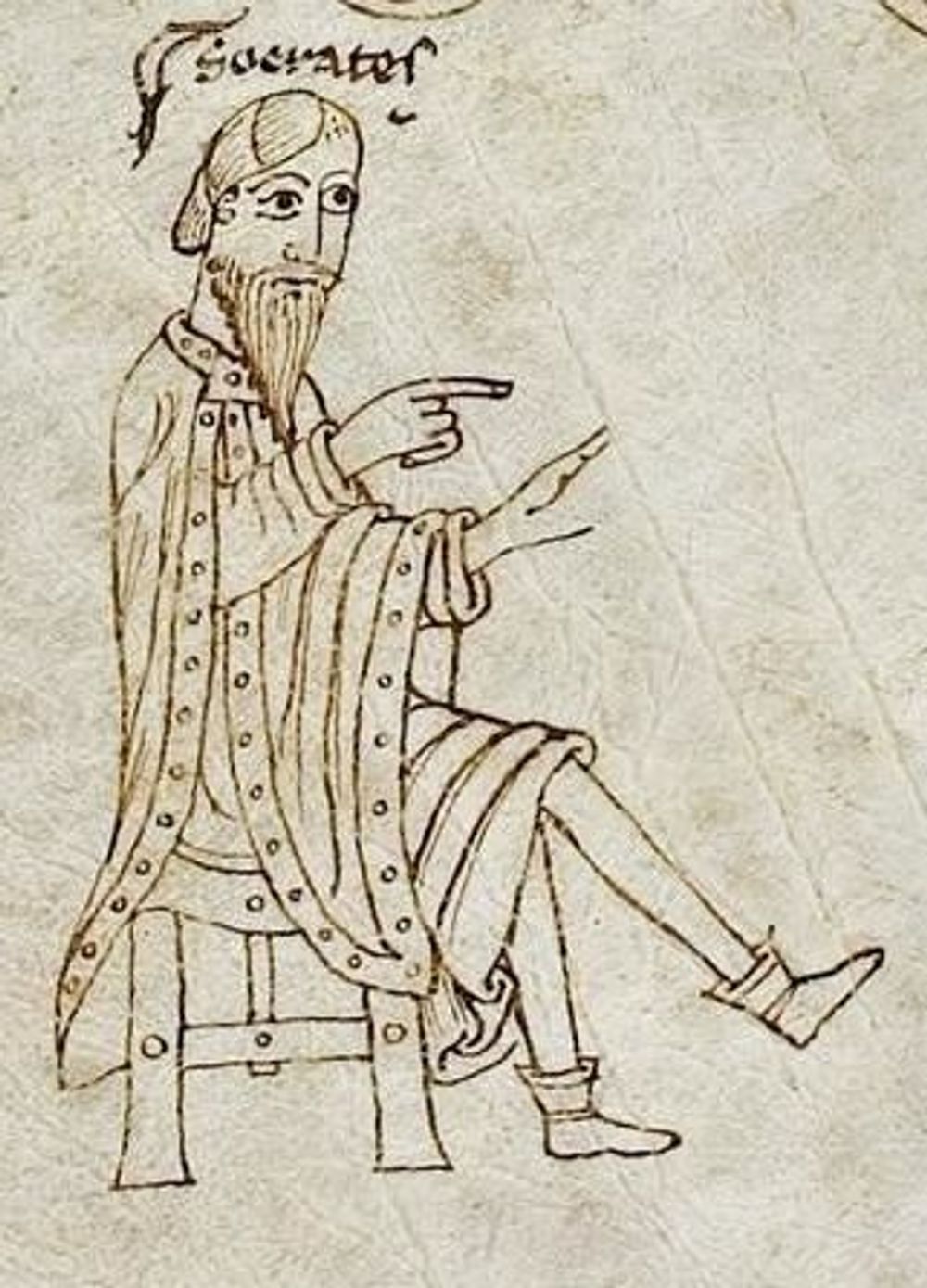
http://tudigit.ulb.tu-darmstadt.de/show/Hs-2282
The ‘Porphyrian Tree’
Porphyry, a third-century Greek philosopher, wrote the Isagoge, an introduction to Aristotle’s Categories. This work was later translated into Latin and commented upon by Boethius. One of the key contributions of this work was a treatment of the first, and most important, of Aristotle’s categories – substance. Porphyry investigated what substance consisted of by using differentiae2 – looking at the essential features which distinguished one species within a genus3 from another. This process of distinguishing between genera was often visualised in medieval manuscripts in the form of a tree diagram. The ‘Porphyrian tree’ is a schematic tool used to divide a category, genus, into its constituents, and in so doing work out what the sub-genera and species which make up this category consist of. It is a tool for thinking about what things are and so working out the essential characteristics of particular species. Although there is no evidence that Porphyry himself came up with this schematic device, it’s most commonly associated with manuscripts of his Isagoge.
The Tree uses ‘differentiae’, points of distinction, to evaluate what a substance is. In this manuscript of the Isagoge (Einsiedeln, Stiftsbibliothek, Cod. 315 (605)) the tree is worked out to a particular conclusion, to identify the characteristics of a human being. Starting from the top, we establish that we are dealing with a corporeal substance, which is animate, capable of sensation, rational and mortal. The examples provided here of ‘human beings’ are the philosophers Socrates, Cicero and Plato.
Substance: corporeal / incorporeal
Corporeal: animate / inanimate
Animate: sensate / insensate
Animal: rational / irrational
Rational animal: mortal / immortal
Man: Socrates / Cicero / Plato
_p53.jpg)
_p53.jpg)
We can use the Tree to identify features of other substances. For example, using this same terminology we could describe a dog as a corporeal, animate, sensate, irrational substance. A flower is a corporeal, animate, insensate, substance. A rock is an incorporeal, inanimate substance. The Porphyrian tree permits the user to identify the essential characteristics of everything in the world. All of Aristotle’s categories could be expanded into ‘trees’ using the same process of differentiation, but the category of substance was the one which was most commonly described in this form.
In this version of the Porphyrian tree the examples given of ‘homo’, ‘man’, at the bottom of the tree are Plato, Cato, and Cicero. These names would have been evocative for the medieval reader. Plato’s name signified the discipline of philosophy. Cicero’s signified rhetoric, while Cato’s Distachs was a widely-used elementary textbook for learning Latin, and so evoked the art of grammar.

https://www.e-codices.unifr.ch/en/list/one/sbe/0029
The Porphyrian tree was co-opted into different textual contexts. In this example, a version of the tree is incorporated into a thirteenth-century manuscript of John of Damascus’s Logica (Paris, BnF, MS lat. 16598, f. 37r). This manuscript was donated to the library at the Sorbonne by Gerard d’Abbeville, a thirteenth-century master. Here, as might befit a book belonging to a theologian, Peter and Paul take the place of Plato and Socrates as examples of the species ‘man’.


Leaves, branches, even flowers, were added to Porphyrian tree diagrams, in spite of the fact that, unlike its organic counterpart, it ‘grows’ (or is read) from top to bottom.
In this manuscript (Paris, BnF, lat. 12949), a copy of De decem categoriae, a text on the categories attributed in the medieval period to Augustine, a branching diagram, complete with foliate details and similar to a Porphyrian tree, has been added in the margin.


The tradition of referring to the ’Porphyrian tree’ explicitly as a tree can be traced back to the thirteenth century. The famous logical text book, Summulae logicales by Peter of Spain, referred to an ‘arbor Porphyriana’ and copies of the text were frequently illustrated with elaborate depictions of the Porphyrian tree – complete with leaves and branches.
In this example (which like Paris, BnF, lat. 16598 was also part of the bequest of Gerard d’Abbeville to the library of the Sorbonne in the thirteenth century) we can see that the diagram is replete with foliate detailing, with ‘homo’, man, placed at the root of the tree.
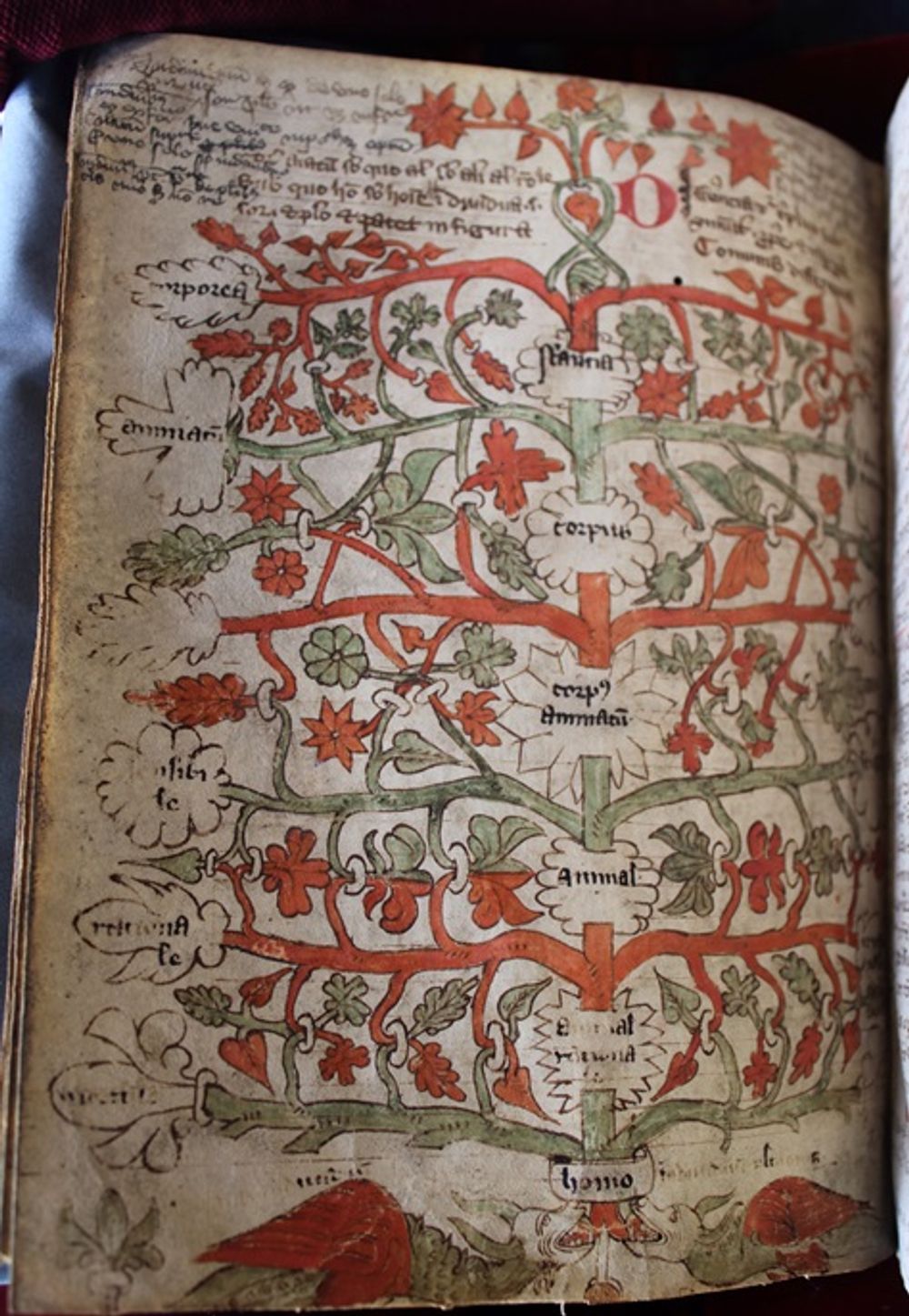
https://gallica.bnf.fr/ark:/12148/btv1b90768515
The Porphyrian tree was just one example of how medieval scholars used visual tools to grapple with thinking about the nature of being, a tradition which extends back to the Carolingian period. In these two copies of Martianus Capella’s De nuptiis Philologiae et Mercurii, a small marginal diagram is appended to the section on dialectic. Circular in form, at its centre it has the word ‘homo’, ‘man’ then ‘animalitas’, ‘ratio’, ‘mortalitas’, ‘sensus’ – animality (i.e. being animate), reason, mortality and sensation – in the next circle. In the outermost circle we find the words ‘lapis’ (stone); ‘equus’ (horse); ‘arbor’ (tree) and ‘angelus’ (angel).
Starting in the centre and reading outwards one can conclude the following:
- that man differs from a stone as he is animate
- that man differs from a horse as he has reason
- that man differs from a tree as he can feel
- that man differs from an angel as he is mortal

http://hdl.handle.net/1887.1/item:1618282

http://hdl.handle.net/1887.1/item:2028417
This scheme, inserted on a slip into a copy of the De decem categoriae also tackles the subject of substance (here termed ‘oycia’, Latinising οὐσία, and described as the ‘genus generalissimum’, the genus of all genera). The left side of the scheme deals with the genus 'tree’, giving the example of a nut-bearing tree as a species of this genus. The right-hand side of the scheme deals with the genus ‘stone’, giving the precious stone beryl as a species of this genus. The central branch of the scheme deals with the genus ‘animal’, with ‘man’ (again citing Cicero) given as the example of its species. Animal, trees and stones are all types of substance but each have different distinguishing qualities.


In this image, taken from the Breviculum of Ramon Llull, other mnemonic devices – namely ladders and towers (which permitted the presentation of partition and progression) – are used alongside a device (to the left of the image) which is reminiscent of the Porphyrian tree. Deus, God, is presented at the top of a scala natura, a ‘ladder of nature’, to the right of the pseudo-tree. To its left are depicted nine wise men, each asking a question – utrum? quid? de quo? quare? quantum? quale? quando? ubi?, quo modo, cum quo?– Whether? What? Of which? By what? How much? Which? Of what kind? When? Where? In what manner, with whom? These ten questions, which can be asked of all substances, were derived by Lllull from a work by the Islamic philosopher, Ibn Sab’in (1217/18–69/71).

https://nbn-resolving.de/urn:nbn:de:bsz:31-8765
Sources used for this contribution:
- Carruthers, M., The Book of Memory (Cambridge, Cambridge University Press, 2008)
- Jeauneau, E., ‘Pour le dossier d’Israël Scot’, Archives d'histoire doctrinale et littéraire du moyen âge, 52, (1985), 7-71
- Lohr, C., ‘The Arabic Background to Ramon Lull’s “Liber Chaos” (ca. 1285), Traditio, 55 (2000), 159-70
- Londy, D. and Johanson, C., Philosophia antiqua: The logic of Apuleius (Leiden, Brill, 1987)
- Parsons, T., Articulating Medieval Logic (Oxford, Oxford University Press, 2014)
- Rouse, R. H., ‘Manuscripts belonging to Richard de Fournival’, Revue d'histoire des textes, 3 (1974), 253-269
- Verboon, A., ‘The Medieval Tree of Porphyry: An Organic Structure of Logic’, in A. Worm and P. Salonis (eds), The Tree. Symbol, Allegory and Structural Device in Medieval Art and Thought (Turnhout, Brepols, 2014), 83-101
Contribution by Irene O’Daly.
Cite as, Irene O’Daly, “Squares and trees”, The art of reasoning in medieval manuscripts (Dec 2020), https://art-of-reasoning.huygens.knaw.nl/trees. ↑Differentiae are characteristics which distinguish one grouping of things from another. In philosophical terms they are ‘predicated’ of things. ↑
A genus (pl. genera) is a grouping of things sharing a particular characteristic (e.g. having substance). A genus can consist of sub-genera; in the case of substance, for example, things which are corporeal and things which are not corporeal etc., and ultimately these genera can be further divided into additional genera and, finally into species, (e.g. human) groupings, which are not genera for anything else and cannot be further divided. ↑



 Next Read:
Next Read: